01  | INTRO
02  | GRAPHS
03  | CONNECTIONS
04  | ABSTRACTIONS
05  | RECOMMENDATIONS
06  | OUTTRO

00  »  beatspixelscodelife.com
02.01 02.02 02.03 02.04 02.05
At the heart of the del.icio.us.discover visualizations is an individual user's graph, a representation of their link-space.

The graphs in this set of experiments/visualizations are tag-agnostic; tags on any link are not taken into account, although one could easily imagine various ways to integrate tag pruning/filtering/matching to assist in searching, or setting the seed directions for an 'information stroll'.

 One other obvious element at work is time. These are merely snapshots for a given time period (in this case, the beginning weeks of March, 2006) and one cannot step in the same collaborative link-space river twice (or even once, really).

Every hugely popular link started with one posting and a new link that has 1 person considering it important may have 1000 people within a week. Due to the nature of the link-space and the curves that fall out of it, the temporal aspect of these graphs is not of great concern, although there are many interesting predictive ideas to explore.

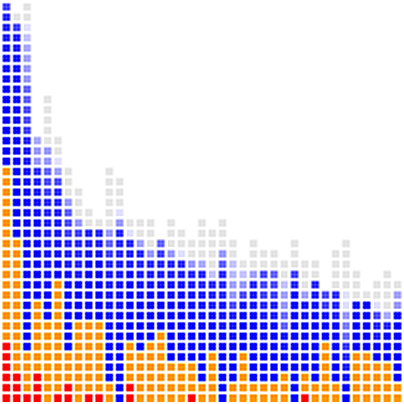
The graph in Figure 02.02 is a representation of my (kiddphunk) del.icio.us link-space.

Each column of colored squares represents a different del.icio.us user. The 10 pixel x 10 pixel squares that form the body of the columns each represent a particular link from that user's link-space that had intersected my link-space. The leftmost column with the solid bar is a stack of my links, with the height of each square compressed down to 1 pixel to save space.

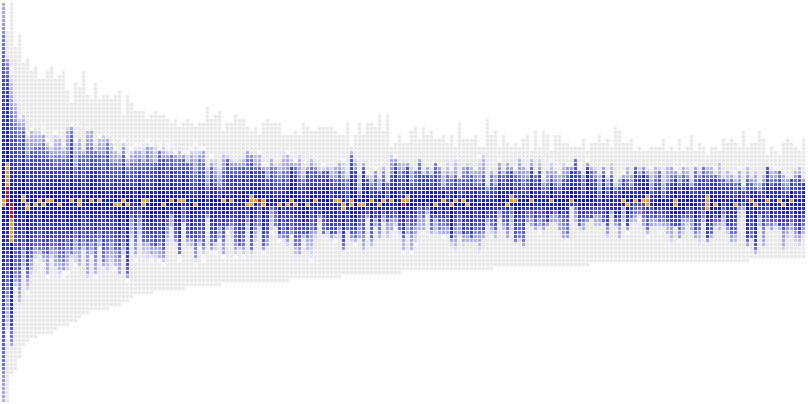
I can now sort by total number of links matched and graph in descending order. This creates a characteristic power-law distribution curve that will be discussed in greater depth shortly.

The internal algorithm works simply by looking at every link that the main user has book-marked, and hashing all of the users who have also book-marked this same link. However, more interesting than the degree of overlap between del.icio.us users' link-space is the degree of popularity for a given link, especially when considering the "sweet spots". The colors in this particular graph (02.02) plot links of a popularity number 'P' (the number of other people linking to the same link) using the following formula:

common = grey = (P > 1000)
popular = blue = (20 < P <= 1000)
 semi-popular = orange = (3 < P <= 20)
 random = red = (P <= 3)

(I'm not implying anything about the actual popularities by these arbitrary lines in the sand; they are however, easy to remember general-level names.)

The link squares are now colored to match popularity and within each column are further sorted with the most popular links at the top in grey, followed by a gradiented blue representing the "middle ground", then the more random (less-popular) links at the bottom in orange and finally red.

A simple weighting algorithm was utilized to 'bubble up' users who matched more of the less-popular links (those in red/orange). The first weighted sorting variant I utilized gave a score of 1 was given for grey links, 2 for blue, 3 for orange and 4 for red. The results of this sorting method is shown for user REAS in Figure 02.03 above. Another weighting method experimented with only assigned scores to links in the red/orange set. Additionally tweaking the thresholds for grey/orange/red in conjunction with various sorting methods gives finer grained control for different visualizations.

One optimization that I did not have time to implement were sorting modes that found users with higher internal red/orange matching percentages by considering the total number of links in an individual's link-space.

Figure 02.04 above shows four user graphs, all recognizably power law distributions. While at first this surprised me, after researching more about power laws and scale-free networks I find this now intuitively sound.

"What matters is this: Diversity plus freedom of choice creates inequality, and the greater the diversity, the more extreme the inequality... The very act of choosing, spread widely enough and freely enough, creates a power law distribution."

(Excerpt from Power Laws, Weblogs, and Inequality,
see also Wikipedia Scale-free networks for more background information on social networks and the power law distribution.)

This is an important feature to note because it means that the top N user's intersections cover a much wider span of links (which may in turn imply a good future predictive capacity for that user, especially when coupled with an appropriate sorting algorithm) than the next N users.

So a rather small sampling of users taken in the form of monitoring their 'link stream' or as an on-demand summary could give a fairly decent sampling of interesting links based on past link history, assuming an adequate amount of information has been accumulated.

 

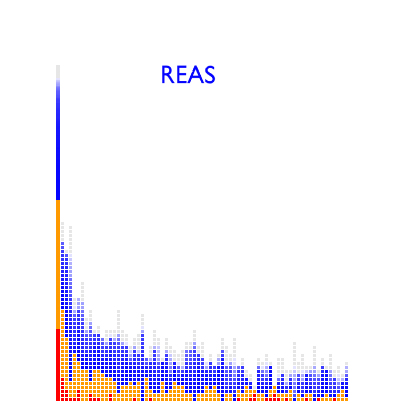
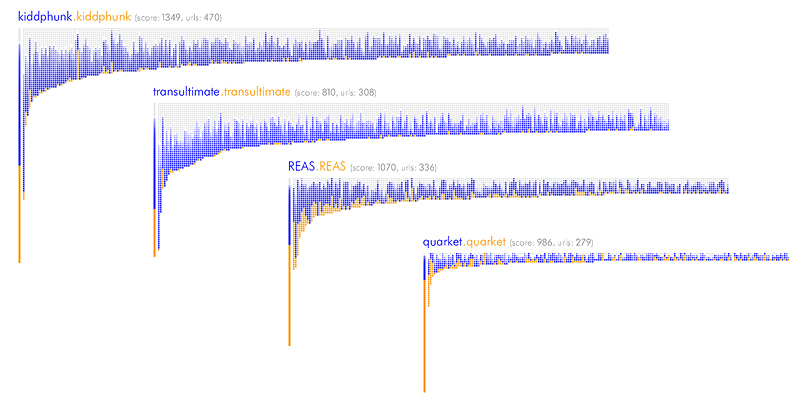
In addition, while Figure 02.04 lacks a value for the red parameter in this particular rendering, a quick comparison of curves still affords a few general observations:

* quarket has the highest proportion of less-popular links (the orange) than REAS, who in turn has a higher orange proportion than kiddphunk.

* while quarket and REAS have roughly the same number of book-marks in their respective link-spaces and a very roughly similar amount of less-popular links, quarket overall has much less area under the curve, implying that many of the less-popular links were not shared with anyone else or are very widely distributed across a wider range of users.

Above, Figure 02.05 shows a section of a graph of transultimate's link-space, with a red/orange weighted sort on the top and a url-count weighted sort on the reflected bottom.

Continue on to part 03 | Connections